Ik heb een nieuwe wiskundige functie bedacht
 

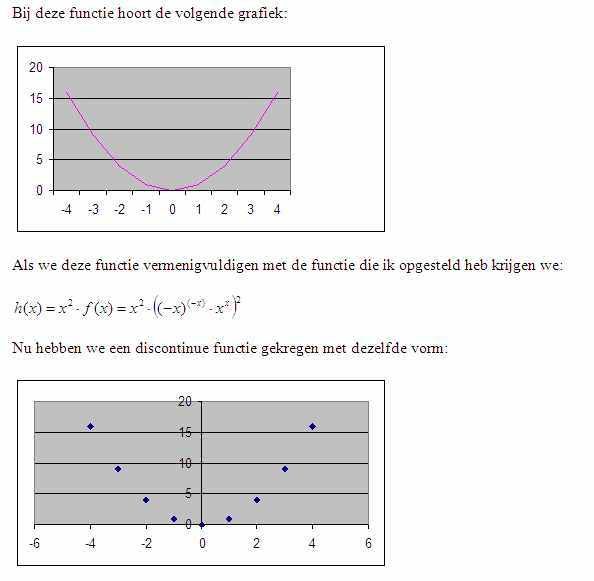Ik hoop dat jullie het begrijpen :)

8O

Ik stel voor dat we deze opstoot van de ziekte genaamd wiskunde trachten in te dijken. :twisted:

Ik moet hem overigens nog verder uitwerken.

Ik stel voor dat je je functie gewoon terug opbergt en in het vervolg via de stelling van Rolle tot dezelfde, doch sneller berekende oplossing komt.

En wat is hier de functie van?

Hoe zou de afgeleide ervan luiden? :-)

Het is besmettelijk! 8O

wiskunde is echt zo iets voor simpele mensen.
opgewonden raken van cijfertjes en formuletjes.
zo'n mensen moeten nogal een rijk geestesleven hebben.

Dat kan tellen! 8O

De functie bestaat enkel in aparte punten, dus er is nergens een afgeleide.

Nu weten we meteen ook waar je zo druk mee bezig was in de week waar we allemaal op u aan het wachten waren :wink:

oeh ja, wiskundigen 'simpel' noemen.
da's durven hé.

Bewijs eerst maar eens dat de functie discontinue is als x < 0 is. Want dat is volgens mij helemaal niet zo. Je kan overal differentiëren.

Waarom al die trukerijen uithalen om het domein van de functie te beperken?

Zet gewoon als functievoorschrift:

h(x) = x^2 voor gehele x
ongedefinieerd voor alle andere x

en klaar.

Vade retro, eh, Mathematica! 8O

Ja, kom maar eens naar het bord gij.

x*x^(x-1)*1 = x^x
f'(x) = f(x) ?
edit: niet dus...

Hier is eigenlijk niets nieuws aan.

Ja, meester. :-(