Citaat:
Oorspronkelijk geplaatst door Savatage
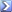
Dat is niet nodig om:
1) het concept achter afgeleiden te snappen
2) afgeleiden te kunnen toepassen
Laat die formule liever achterwege totdat je begint met die bewijzen (waarvoor je ze idd nodig hebt). Die formule biedt geen enkele meerwaarde voor iemand die op zoek is naar wat afgeleiden zijn of het wilt toepassen. Let wel, ik zeg niet dat die formule onbelangrijk of misbaar is, maar het is voor mij een schoolvoorbeeld van hoe men iets duidelijk en simpel veel moeilijker voorstelt dan het is in de wiskunde.
|
Natuurlijk. Eerst begint ge met een tekeningske van een functiegrafiek natuurlijk, en gaat ge een "vergrootglas" gebruiken om altijd maar een kleiner stukje van die grafiek uit te vergroten.
De afgeleide is dan lokaal gezien de benadering van die kromme, die aangeeft hoeveel de waarde van f(x) toeneemt als x toeneemt.
Je kan je de vraag stellen: ik heb een functie f maar ik geef je de formule niet. Je mag mij wel waarden van x geven, en ik zal antwoorden welke waarde f(x) is. Hoe zou je die afgeleide voor x = 5 dan uitvissen ? Welke vragen zou je mij stellen ?
En je komt dan natuurlijk uit op die formule