[patrickve]

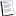
Allez, als kers op de taart, het beetje wiskunde dat aangeeft dat er zelfs geen 'verborgen kost voor anderen' is. Het is gesteund op het feit dat alle marktspelers evenwaardig zijn, en er geen "uniek laatste" vrager is, die verantwoordelijk is voor de extra vraag, maar dat ELK van die spelers een "laatste vrager" kan zijn.

Laten we aannemen dat er N marktspelers zijn "voor", en N+1 marktspelers "na". "x" is de totale hoeveelheid gerealiseerde vraag "voor" en daar komt y bij door de N+1ste marktspeler. Maw, "na" is de vraag gelijk aan x+y.

We hebben dat de totale sociale kost voor gelijk is aan x * c(x).
De totale sociale kost "na" is gelijk aan (x+y) * c(x+y).

Als we aannemen dat y klein is ten aanzien van x, kunnen we c(x+y) schrijven als c(x) + y * dc/dx (eerste orde benadering).

Dan is de totale sociale kost gelijk aan x * c(x) + y * c(x) + x * y * dc/dx + y^2 dc/dx.

We zien dus, dat wanneer er N+1 spelers zijn, en daardoor de vraag met y toenam, de VERHOGING van de sociale kost gelijk is aan:

y * c(x) + x * y * dc/dx + y^2 dc/dx

Maar wat is de prive prijs betaald door die N+1 de speler ? Is dat y * c(x) ? Nee, het is eigenlijk y * c(x+y). En we kunnen hier ook c(x+y) vervangen door c(x) + y * dc/dx.

Dus wordt de prijs, betaald door EEN marktspeler (de N+1ste, maar elke):

y * c(x) + y^2 * dc/dx

De prijs, betaald door EEN van de N+1 marktspelers, die een vraag y heeft, is dus niet gelijk aan de verhoging van de totale sociale kost: er mankeert de term x * y * dc/dx. Dat is wat die fameuze "externality" zou zijn.

Maar dat komt omdat we die 'burden' op EEN MARKTSPELER willen leggen. Terwijll het gegeven dat er N+1 marktspelers zijn, NIET VAN EEN MARKTSPELER komt, maar van de N + 1 marktspelers ! Elk van hen is "deels" de N+1 ste marktspeler. Ze zijn allemaal evenwaardig.

En wat betekent dat ? Het betekent dat het NORMAAL IS dat elk van de N+1 marktspelers voor 1/(N+1) de kosten moeten dragen van "er te zijn". Er is niet ene die "er bij kwam". Ze hebben allemaal samen beslist van "met N+1 te zijn". Er moet dus niet een enkele opdraaien voor die extra kost van met N+1 te zijn.

Laten we ervan uit gaan dat x = N * y. Ttz, elk van de marktspelers draagt dezelfde vraag bij, ZOALS de N+1ste speler.

Toen ze nog met N waren, betaalden ze dus elk y * c(x). Maar nu betalen ze y * c(x+y) = y * c(x) + y^2 * dc/dx.

Elk van hen heeft nu dus een extra kost van y^2 * dc/dx. We hadden die term al in rekening gebracht voor de N+1ste speler.

De "kost" die die teweeg bracht en die zogezegd een "externality" was, die niet door hem opgehoest werd, was gelijk aan:

x * y * dc/dx.

Maar we hebben gezegd dat ELK van de N overige spelers eigenlijk voor 1/N OOK verantwoordelijk is voor het gegeven dat er nu N+1 zijn: elk van hen had immers ook de N+1de speler kunnen zijn.

En wat gebeurt er als we die "externality" nu delen door die N overige, equivalente, spelers ?

x * y * dc/dx / N = (x/N) * y * dc/dx. En rarara, wat is x/N ? Dat is y.

Dus hebben we dat de extra kost, als we die door N delen om die eerlijk te verdelen over ELK VAN DE POTENTIELE "N+1" de spelers:

y^2 dc/dx.

En dat is EXACT wat elk van hen nu meer betaalt.

Maw, de "rekeningen kloppen".

Als de file van N naar N+1 gaat, is ELK VAN DIE WAGENS potentieel de extra N+1 de wagen. Als we de extra sociale kost van van N naar N+1 te gaan, equitabel verdelen over elk van die wagens, die elk de N+1 de is, dan zien we dat de "marktprijs" c(x+y) die kost exact in rekening brengt.

Iedereen betaalt zijn eigen deel om potentieel de N+1 de te zijn.

Het is niet omdat gisteren Jan, Marie, en Piet beslisten van de auto te nemen, en vandaag Jan, Marie, Piet EN JEFKE beslissen van de auto te nemen, dat JEFKE uiteraard de volle extra pot moet betalen. Jan, Marie en Piet hebben evenveel hun deel in de file van vandaag, dan Jefke. En als je de extra kost door alle deelnemers deelt, dan vinden we dat de rekeningen perfect kloppen, en dat alle "schuldigen" hun deel bijdragen aan de kost van de file.

Er is dus zelfs geen externality ook al zou je de verhoging van de marktprijs/kost als dusdanig willen beschouwen. Dat komt enkel van de rederingsfout dat enkel Jefke schuldig is om de N+1ste te zijn.

Voor natuurkundigen doet dat denken aan de Gibbs paradox maar dan veel simpeler.