
Problemen met registreren of reageren op de berichten?
Een verloren wachtwoord?
Gelieve een mail te zenden naar [email protected] met vermelding van je gebruikersnaam.
 |
Registreren kan je hier. Problemen met registreren of reageren op de berichten? Een verloren wachtwoord? Gelieve een mail te zenden naar [email protected] met vermelding van je gebruikersnaam. |
|
|||||||
| Registreer | FAQ | Forumreglement | Ledenlijst |
| Over koetjes en kalfjes... Op verzoek van de gebruikers van dit forum: een hoekje waarin je over vanalles en nog wat kan praten... De boog moet namelijk niet altijd gespannen staan hé. |
 |
|
|
Discussietools |
|
|
#1 |
|
Staatssecretaris
Geregistreerd: 18 november 2005
Berichten: 2.691
|
vrede,
het is eigenlijik simpel: neem een voldoende grote bokaal. begin met stap 1: gooi 1 wit bolletje en 10 zwarte bolletjes in de bokaal wacht een uur en herhaal stap 1 wacht een half uur en herhaal stap 1 wacht een kwartier en herhaal stap 1 wacht zeven en een halve minuut en herhaal stap 1 ... (blijf dit herhalen, wacht telkens half zo lang als de vorige keer en herhaal stap 1) we gaan er nu even van uit dat stap 1 in totaal 0 sekonden tijd kost, in dat geval heb je twee uur na het begin van het experiment, stap 1 oneindig vaak herhaald. haal nu 1 willekeurig bolletje uit de bokaal, hoe groot is de kans dat het wit is? (een variante kunnen we doen met stap 2: gooi 1 wit bolletje en 1 zwart bolletje in de bokaal en haal er meteen 1 zwart bolletje weer uit. hoe groot is de kans nu dat je op het einde een wit bolletje trekt). het antwoord is telkens wiskundig af te leiden en dus exact bepaalbaar, maar het gaat ook telkens een beetje tegen onze intuïtie in. het is dus een ideale puzzel om eens op een familiefeest voor te leggen aan nonkels en tantes. discussie verzekerd! een beetje zoals het monty-hall probleem zeg maar. vrede, korneel
__________________
DENK EROM: EIGEN KARMA EERST! ALTIJD, OVERAL! |
|
|

|
|
|
#2 |
|
Secretaris-Generaal VN
Geregistreerd: 21 januari 2007
Locatie: Vlaanderen
Berichten: 84.071
|
In mijn familie gaan ze er zich niet met bezighouden denk ik
__________________
PBL-RKT
Undefeated Army Bietan Jarrai |
|
|

|
|
|
#3 |
|
Eur. Commissievoorzitter
Geregistreerd: 25 april 2006
Locatie: Zeeuws-Vlaanderen
Berichten: 9.152
|
Een familiefeest zónder discussie zou voor de verandering eens aangenaam zijn...
__________________
The problem with quotes on the Internet is that it is hard to verify their authenticity - Abraham Lincoln |
|
|

|
|
|
#4 | ||
|
Perm. Vertegenwoordiger VN
Geregistreerd: 28 juli 2004
Locatie: aan lager wal
Berichten: 13.961
|
Citaat:
__________________
Citaat:
|
||
|
|

|
|
|
#5 |
|
Staatssecretaris
Geregistreerd: 18 november 2005
Berichten: 2.691
|
vrede,
vandaar een wiskundig puzzeltje, zo gaat de discussie eens ergens anders over. en een poging tot antwoord? vrede, redwasp
__________________
DENK EROM: EIGEN KARMA EERST! ALTIJD, OVERAL! |
|
|

|
|
|
#6 |
|
Secretaris-Generaal VN
Geregistreerd: 26 maart 2008
Locatie: Kempen
Berichten: 22.730
|
had we ever?
__________________

|
|
|

|
|
|
#7 |
|
Secretaris-Generaal VN
Geregistreerd: 28 augustus 2007
Berichten: 21.733
|
Een leuker wiskundig spelletje, als er kinderen (tieners) bij zijn, vind ik de volgende:
Neem 16 lucifertjes. Het spel bestaat eruit dat 2 spelers, om beurten, tussen 1 en 4 lucifers wegnemen. Degene die de laatste lucifer wegneemt verliest. Je laat grootmoedig de andere partij beginnen, aangezien de eerste altijd verliest. Dat komt omdat je de trekking van je voorganger steeds aanvult tot 5. Neemt hij 1 dan neem jij 4, neemt hij 2 dan jij 3 enz.... zo kom je altijd aan 15 na 3 beurten en zit hij met de laatste. Leuk om te zien wie het door heeft en na hoe lang. |
|
|

|
|
|
#8 |
|
Europees Commissaris
Geregistreerd: 30 november 2010
Berichten: 6.617
|
Doet mij denken aan dat andere bekende raadsel:" waar is die 1 euro naartoe"? De meesten kennen dit raadsel wel: 3 vrienden gaan op hotel. Ze nemen elk een kamer apart. De prijs per kamer bedraagt 9 euro. Elk van hen betaalt met een briefje van 10 euro . De receptionist , aan wie ze het geld overhandigen, bedenkt zich plots dat er die bewuste dag een promotie plaatsvindt: 3 kamers boeken voor slechts 25 euro. De 3 vrienden hebben dus 5 euro teveel betaald. Omdat de receptionist dit bedrag niet eerlijk onder de 3 vrienden kan verdelen, geeft hij elk van hen 1 euro terug. De overige 2 euro steekt hij gewoon in z'n zak. Nu is de vraag (discussie gegarandeerd op ieder feestje): omdat elk van de 3 gasten 1 euro terugkreeg op hun briefje van 10, betaalde elk 9 euro.
Er werd dus 3x 9 euro betaald= 27 euro. Doch, oorspronkelijk was er 30 euro betaald, waarvan de receptionist er 2 in z'n zak stak. Dus: 27 euro betaald + 2 euro in de zak=29 euro. Waar is die 1 euro gebleven om de som compleet te maken? Zeker dat al uw nonkels, buren, neven , tantes hierover een andere theorie hebben! |
|
|

|
|
|
#9 |
|
Secretaris-Generaal VN
Geregistreerd: 26 maart 2008
Locatie: Kempen
Berichten: 22.730
|
Bij ons familie, simpele mensen dat we zijn, spelen we alle jaren portretje of 'beeld het spreekwoord, zegswijze, bekende bijbelse citaten uit.'
Dan hebt je al jaren dezelfden die elkander zo hard mogelijk willen kloten, met de moeilijkste -bekende- bijbelse citaten te verzinnen, die de ander dan moet uitbeelden. Zo uitbeelden dat duurt ongeveer een half uur de man, 4 keer een half uur voor die 4 klootzakken en dan 5 minuten per volgende man. Ook abstracte begrippen uitbeelden doen het goed. Echter is het publiek geoefend en hebben ze begrippen zoals 'zwaartekracht' en 'pi' nogal tamelijk snel door. Het beste dit jaar was beeld uit "De dialectiek van Plato."
__________________

|
|
|

|
|
|
#10 |
|
Minister-President
Geregistreerd: 6 juni 2010
Locatie: in Lalaland
Berichten: 4.298
|
tja, het is eens iets anders dan zatte tante Germaine en een nog zattere tante Rachel over een straalbezopen nonkel Roger zien kronkelen op de Twister speelmat.
__________________
 Dwarsliggers zijn nodig.....ze houden de sporen recht . Dwarsliggers zijn nodig.....ze houden de sporen recht .  Live! Laugh! Love! If that doesn't work... ...LOAD! AIM! SHOOT! (repeat if you missed) |
|
|

|
|
|
#11 | ||
|
Minister-President
Geregistreerd: 19 juni 2007
Locatie: Brabant-Dietsland-Avondland
Berichten: 4.254
|
Citaat:
Als ik mij niet vergis althans... Citaat:
|
||
|
|

|
|
|
#12 | ||
|
Perm. Vertegenwoordiger VN
Geregistreerd: 12 augustus 2006
Berichten: 17.805
|
Citaat:
Maar dat klopt volgens mij niet hoor... gewoon 1/11 kans op een witte lijkt me logischer.
__________________
Citaat:
|
||
|
|

|
|
|
#13 | ||
|
Europees Commissaris
Geregistreerd: 3 april 2010
Locatie: planeet aarde
Berichten: 7.276
|
Citaat:
Citaat:
Zo neen, 100% kans op een wit bolletje. Zo ja, 1/6, want tellen we de steeds herhalende twee stappen op, dan hebben we telkens 1+1=2 witte bolletjes en 10+1-1=10 zwarte bolletjes. Weer hetzelfde verhaal met de gelijk blijvende verhoudingen, 2/12=1/6. |
||
|
|

|
|
|
#14 | ||
|
Perm. Vertegenwoordiger VN
Geregistreerd: 12 augustus 2006
Berichten: 17.805
|
Citaat:
Mss is het fout; redwasp?
__________________
Citaat:
|
||
|
|

|
|
|
#15 | |
|
Europees Commissaris
Geregistreerd: 3 april 2010
Locatie: planeet aarde
Berichten: 7.276
|
Citaat:
EDIT: Voor het geval mijn iemand uitleg over de regel van l'Hôpital niet duidelijk vond. De regel luidt: Als voor twee differentieerbare functies f en g, en een waarde c geldt, dat:  of  , ,dan geldt: 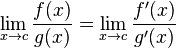 indien de limiet aan de rechterzijde bestaat. Laatst gewijzigd door Robinus V : 2 januari 2011 om 15:10. |
|
|
|

|
|
|
#16 | ||
|
Perm. Vertegenwoordiger VN
Geregistreerd: 12 augustus 2006
Berichten: 17.805
|
Citaat:
__________________
Citaat:
|
||
|
|

|
|
|
#17 | |
|
Secretaris-Generaal VN
Geregistreerd: 4 oktober 2005
Berichten: 21.225
|
Citaat:
Laatst gewijzigd door Kallikles : 2 januari 2011 om 15:15. |
|
|
|

|
|
|
#18 |
|
Secretaris-Generaal VN
Geregistreerd: 4 oktober 2005
Berichten: 21.225
|
Met dezelfde redenering kunnen we ook de variante oplossen: bij x stappen zullen er x witte bolletjes en 10 zwarte bolletjes zijn en in totaal 10+x bolletjes. De kans om een wit bolletje te trekken is dus de limiet voor x gaande naar +oneindig van x/(10+x) of 1, m.a.w. we zullen zeker een wit bolletje trekken, al zitten er nog 10 zwarte bolletjes in de doos.
Laatst gewijzigd door Kallikles : 2 januari 2011 om 15:27. |
|
|

|
|
|
#19 |
|
Minister-President
Geregistreerd: 6 juni 2010
Locatie: in Lalaland
Berichten: 4.298
|
pppfff amai jullie hebben saaie familiefeestjes.
 lang leve Twister lang leve Twister   lange leve tante Germaine en tante Rachel lange leve tante Germaine en tante Rachel 
__________________
 Dwarsliggers zijn nodig.....ze houden de sporen recht . Dwarsliggers zijn nodig.....ze houden de sporen recht .  Live! Laugh! Love! If that doesn't work... ...LOAD! AIM! SHOOT! (repeat if you missed) Laatst gewijzigd door Vlaamse Leeuwin : 2 januari 2011 om 15:33. |
|
|

|
|
|
#20 | ||
|
Perm. Vertegenwoordiger VN
Geregistreerd: 12 augustus 2006
Berichten: 17.805
|
Citaat:
__________________
Citaat:
|
||
|
|

|