Einstein

[harriechristus]

135 - De inwendige eeuwigheid der tijd.

Wat de tijd betreft moge hierdoor duidelijk zijn dat de mens constant elke willekeurige korte tijdsduur (dus voor een moment van bijvoorbeeld één seconde) door een inwendige eeuwigheid van tijd heen gaat, die ook werkelijk bestaat in een inwendige oneindige reeks van culturen in de microkosmos.
Dus ook zo dat de ene eeuwigheid op de andere volgt en er dus een oneindige reeks van eeuwigheden bestaat.
Dit is natuurlijk totaal onvoorstelbaar, zoals de oneindigheid of eeuwigheid überhaupt onvoorstelbaar is, maar men wel kan begrijpen dat het zo moet zijn.
De oneindigheid is niet voor te stellen, maar wel te begrijpen, want men weet wat daarmede bedoeld wordt.

De onvoorstelbaarheid der abstracte getallen en de meetkunde.

Overigens: niet alleen de oneindigheid is onvoorstelbaar, maar het getal 0 is ook onvoorstelbaar, want het is immers niks.
Verders zijn ook alle abstracte getallen niet voor te stellen. Ik kan me wel 5 appels voorstellen of 3 peren of 10 meter lengte, maar ik kan me de getallen: 5 en 3 en 10 als zodanig niet voorstellen.
Nochtans begrijp ik wat er mee bedoeld wordt.
En niet alleen is de rekenkunde abstract en dus onvoorstelbaar, ook de meetkunde is abstract, want in werkelijkheid bestaat er niet zoiets als een rechte lijn, want deze moet dan oneindig dun zijn en bovendien absoluut recht.
Dat kan ik me niet voorstellen, wel een streep met dikte en bij nadere beschouwing zal die altijd wel wat krom zijn.
Wel kan ik een lijn voorstellen als scheiding van twee vlakken, maar ook dat kan in werkelijkheid nooit zuiver zijn.
Kortom: ook de meetkunde is abstract.

De eindigheid valt niet te bewijzen, terwijl de oneindigheid wel zo logisch is.

Dus dat de oneindigheid niet voorstelbaar is, is geen geldig kriterium, dat deze niet zou kunnen bestaan. Ten eerste bestaat het als idee (kwalitatief), en ook als idee van een getal (kwantitatief) en ten tweede ook in de concrete werkelijkheid in de microkosmos als een oneindige reeks van steeds hogere culturen met een steeds snellere tijd tot in het oneindige.
Dit omdat de logica daartoe dwingt, ook al zou men de oneindigheid feitelijk nooit kunnen bewijzen: dat het heelal eindig zou zijn is ook nooit definitief te bewijzen, want vroeg of laat vind men aan het einde wel weer een nieuw begin, zoals de wetenschappen telkens weer hebben bewezen.
Het is nog niet zo lang geleden dat men dacht dat de atomen de kleinste deeltjes waren.
Nu denkt men dan weer dat Planck het kleinst mogelijke deeltje heeft gevonden met 10^-35 meter, hoewel men bij de Oerknal spreekt van een oneindig kleine grootte voor de Singulariteit als begin daarvan, wat dus eindeloos veel kleiner is.

Een oneindig kleine grootte.

Een oneindig kleine "grootte" is als kleinheid niet te bepalen, want elke bepaling, hoe klein dan ook, is oneindig groot ten opzichte van 0.
Het is echter niet de 0 zelf, want dan zou men dat gewoon kunnen zeggen.
Als object en ook als getal is het dus een tegenstrijdigheid en alleen als begrip te vatten als een beweging naar steeds kleiner, dus naar 0.
Als beweging kan men dan beter het begrip: eindeloos gebruiken.
Het "nadert" dan de 0, wat deels ook onzin is, want zolang het geen 0 is, is het nog steeds oneindig ver van 0 verwijderd.
Anderzijds: als het de 0 kan bereiken in een beweging (bijvoorbeeld in elke ruimtelijke beweging door een ruimtelijk punt heen), dan moet er ook van een naderen sprake geweest zijn vanuit de beperkte visie van een waarnemer, die het hele proces nooit tot in het oneindig kleine zal kunnen volgen en vanuit die beperktheid van een naderen spreekt.
Want zou hij het steeds kleinere bij het naderen kunnen volgen, dan zou blijken dat het steeds kleinere even groot blijft en dus niet nadert.
Het naderen is dus relatief bezien, volhardend vanuit een beperkt standpunt, maar anderzijds absoluut noodzakelijk is om de doorgang door het oneindig kleine te laten voltrekken.
Gaat men mee met het steeds kleinere, dan voltrekt het zich nooit, doordat dan niet alleen de kleinheid, maar ook de tijd niet door eigen oneindige reeks van het steeds kortere heen komt en beiden in het respectievelijke inwendige eeuwige HIER en NU vast blijven zitten, zich daarin als het ware vast boren.

[Rizzz]

Oorspronkelijk geplaatst door harriechristus

dat is dan volkomen onzin, want ik heb je al vele malen getoond dat je er wel mee kunt rekenen.
En dat dat bovendien ook allang gebeurd in de limietberekeningen.

Enkel jij kan er mee rekenen.
En je hebt limietberekeningen verkeerd begrepen zei ik al, "neigen naar oneindig" is niet hetzelfde als "gelijk aan oneindig".

[Rizzz]

Oorspronkelijk geplaatst door harriechristus

Oneindig is niet alleen een kwalitatief idee, maar ook een getal, een hoeveelheid dus, wat heel gemakkelijk te begrijpen is.

Bovendien wordt het ook in de limietberekeningen gebruikt als een hoeveelheid.

Een oneindige reeks is namelijk een oneindige hoeveelheid.


Kan het nog duidelijker?
Heel gemakkelijk te begrijpen als je een beetje verstand hebt.

Dat het echter niet op een rekenmachine staat kan een mechanische oorzaak hebben dat een rekenmachine geen eindeloze reeks kan uitvoeren.
Dat kunnen wij ook niet, maar we kunnen het als getal wel begrijpen.

Bovendien heb ik het even voor je bij Google opgezocht in de Wikipedia:

In de wis- en natuurkunde heeft oneindig een min of meer kwantitatieve betekenis en wordt als symbool voor oneindig een lemniscaat (\infty), of liggende acht, gebruikt.

Ik:

Nu is min of meer wel een rare uitdrukking, wat alleen maar uitdrukt dat de wiskunde nog in onzekerheid verkeert en nog niet helemaal wakker is.
Maar hieruit moge wel duidelijk blijken dat zelfs de Wikipedia het "min of meer" met mij eens is.


http://nl.wikipedia.org/wiki/Oneindigheid

Nog even extra uit de Wikipedia:

Dus is de verzameling natuurlijke getallen, en daarmee ook de even getallen, oneindig.

Ik: Ergo: oneindig is een getal.

Kan het nog duidelijker?.......

Het kan idd. nog veel duidelijker want het blijft gewoon jouw interpretatie.
Ik zal er nog eens een bron bij halen,
Dit is wel duidelijk:

The very sentence "1/infinity = 0" has no meaning. Why? Because "infinity" is a concept, NOT a number. It is a concept that means "limitlessness." As such, it cannot be used with any mathematical operators. The symbols of +, -, x, and / are arithmetic operators, and we can only use them for numbers.

http://mathforum.org/library/drmath/view/62486.html

Zwart op wit.

[harriechristus]

Oorspronkelijk geplaatst door Rizzz

Enkel jij kan er mee rekenen.
En je hebt limietberekeningen verkeerd begrepen zei ik al, "neigen naar oneindig" is niet hetzelfde als "gelijk aan oneindig".

Onzin: de limiet is het bereiken, dus de voltooiing van een oneindige reeks.

Neigen is helemaal geen rekenkundig begrip, dat hoort thuis in de psychologie.

Dus je hebt er zelf niks van begrepen.

[Rizzz]

Oorspronkelijk geplaatst door harriechristus

Onzin: de limiet is het bereiken, dus de voltooiing van een oneindige reeks.

Neen, de limiet wordt nooit bereikt, net omdat de reeks oneindig is.

Een oneindige reeks kan niet "voltooien", nogmaals er is geen "na" da's net de definitie van een oneindige reeks. We zijn weer bij af...

[harriechristus]

Oorspronkelijk geplaatst door Rizzz

Het kan idd. nog veel duidelijker want het blijft gewoon jouw interpretatie.
Ik zal er nog eens een bron bij halen,
Dit is wel duidelijk:

http://mathforum.org/library/drmath/view/62486.html

Zwart op wit.

Daar zijn de wiskundigen het dan over oneens.

Volgens mij is het gewoon een getal en ook de beroemde wiskundige Georg Cantor van de verzamelingenleer werkt met oneindigheden.

En bij de Singulariteit vind ik ook het delen door 0.

http://nl.wikipedia.org/wiki/Singulariteit

In de analyse een horizontale of verticale asymptoot, ofwel een punt waarop een grafiek en/of functie naar een oneindig grote waarde gaat, bijvoorbeeld door zich door nul te delen.

Fout is het dat het naar het oneindige gaat, in plaats dat een deling door 0 gewoon oneindig is.

[harriechristus]

Oorspronkelijk geplaatst door Rizzz

Neen, de limiet wordt nooit bereikt, net omdat de reeks oneindig is.

Een oneindige reeks kan niet "voltooien", nogmaals er is geen "na" da's net de definitie van een oneindige reeks. We zijn weer bij af...

Dat is dan fout, want het wordt wel bereikt, namelijk in ons begrip als ook in de realiteit.

Zou dat niet zo zijn, dan zou je ook niet van 1 naar 2 kunnen tellen, want ook tussen 1 en 2 zit een oneindige reeks.

En zou je ook 0 nooit kunnen bereiken, want 0 is helemaal niks en bestaat dus niet.

[harriechristus]

Oorspronkelijk geplaatst door Rizzz

Het kan idd. nog veel duidelijker want het blijft gewoon jouw interpretatie.
Ik zal er nog eens een bron bij halen,
Dit is wel duidelijk:

The very sentence "1/infinity = 0" has no meaning. Why? Because "infinity" is a concept, NOT a number. It is a concept that means "limitlessness." As such, it cannot be used with any mathematical operators. The symbols of +, -, x, and / are arithmetic operators, and we can only use them for numbers.

Zwart op wit.

Dit wordt zomaar beweerd zonder enige logische onderbouwing.

Het heeft dus geen enkele waarde dan een willekeurige en ook zeer domme mening te zijn.

[harriechristus]

Oorspronkelijk geplaatst door Rizzz

Neen, de limiet wordt nooit bereikt, net omdat de reeks oneindig is.

Een oneindige reeks kan niet "voltooien", nogmaals er is geen "na" da's net de definitie van een oneindige reeks. We zijn weer bij af...

Dus als de limiet gelijk is aan 2, dan wordt 2 nooit bereikt en moeten we het getal 2 afschaffen?

[Rizzz]

Oorspronkelijk geplaatst door harriechristus

Dus als de limiet gelijk is aan 2, dan wordt 2 nooit bereikt en moeten we het getal 2 afschaffen?

Een beetje verward harrie?
Ik dacht dat we het over limieten naar oneindig hadden?
http://www.mathsisfun.com/calculus/limits-infinity.html

[Rizzz]

Oorspronkelijk geplaatst door harriechristus

Dit wordt zomaar beweerd zonder enige logische onderbouwing.

Het heeft dus geen enkele waarde dan een willekeurige en ook zeer domme mening te zijn.

Zoals steeds, jij bent degene die een hele rare stelling maakt die compleet in gaat tegen alles wat de wiskunde ons leert, jij bent degene die beweert dat alle rekenmachines ter wereld verkeerd zouden geprogrammeerd zijn.
En dan zou het aan mij zijn om mijn zaak te onderbouwen? Wat ik en anderen trouwens op alle mogelijke manieren hier gedaan hebben. We hebben langs alle kanten gaten in je theorie geprikt, die van Alboreto was nog de meest duidelijkste.

[harriechristus]

Oorspronkelijk geplaatst door Rizzz

Een beetje verward harrie?
Ik dacht dat we het over limieten naar oneindig hadden?
http://www.mathsisfun.com/calculus/limits-infinity.html

Daar heb ik het ook over: wat is de limiet van de oneindige reeks van: 1 + 1/2 + 1/4 + 1/8 + enzovoort tot in het oneindige?

Elk getal kan namelijk het limiet zijn van een oneindige reeks.

[harriechristus]

Oorspronkelijk geplaatst door Rizzz

Zoals steeds, jij bent degene die een hele rare stelling maakt die compleet in gaat tegen alles wat de wiskunde ons leert, jij bent degene die beweert dat alle rekenmachines ter wereld verkeerd zouden geprogrammeerd zijn.

Dat is onzin, want de wiskunde leert ons de oneindige reeks van natuurlijke getallen van 0 tot oneindig.
Nu zijn er nog steeds mensen die denken dat de 0 daar niet bijhoort en andere dat het oneindige er niet bij hoort.

Verder raad ik je aan eens Georg Cantor te lezen, de vader van de verzamelingenleer.

Goed: dat een rekenmachine niet tot het oneindige kan tellen, daar kan ik me iets bij voorstellen, maar ik ben geen techneut.
In ieder gevallen deugen die dingen niet.

En dan zou het aan mij zijn om mijn zaak te onderbouwen? Wat ik en anderen trouwens op alle mogelijke manieren hier gedaan hebben. We hebben langs alle kanten gaten in je theorie geprikt, die van Alboreto was nog de meest duidelijkste.

Ik heb nog geen enkele onderbouwing mogen vernemen, dan een hoop onzinnigheid al zou je van mijnheer pastoor niet door 0 mogen delen.

Puur dogmatisch gedacht dus.

[Rizzz]

Oorspronkelijk geplaatst door harriechristus

Daar heb ik het ook over: wat is de limiet van de oneindige reeks van: 1 + 1/2 + 1/4 + 1/8 + enzovoort tot in het oneindige?

Elk getal kan namelijk het limiet zijn van een oneindige reeks.

Klopt, maar dit:

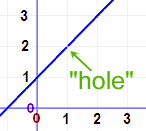en dit: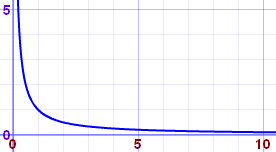


is niet hetzelfde.

In beide gevallen gaat het om limietberekeningen maar in het 2de geval hebben we het over limieten naar oneindig, is dat niet waar we het over hadden?

En in het 2de geval (1/x) is 0 de limiet, niet oneindig.
We zeggen hier, "de limiet van 1/x als x oneindig benadert is 0"
Let op het woordje "benadert", maar niet "bereikt"

zie nogmaals:

As x approaches infinity, then 1/x approaches 0

When you see "limit", think "approaching"

http://www.mathsisfun.com/calculus/limits.html

[Rizzz]

Oorspronkelijk geplaatst door harriechristus

Ik heb nog geen enkele onderbouwing mogen vernemen, dan een hoop onzinnigheid al zou je van mijnheer pastoor niet door 0 mogen delen.

Puur dogmatisch gedacht dus.

We hebben je op vele manieren aangetoond dat als je bewerkingen met oneindig toelaat, of delingen door 0 toelaat in de wiskunde, je allerlei tegenstrijdigheden tegen komt.
Vandaar dat we zeggen dat oneindig geen getal is en je niet mag delen door 0. Simpel toch?

Je kan blijven rond de pot draaien maar het simpele feit blijft dat er geen "na" is in een oneindige reeks, da's per definitie zo, anders is het geen oneindige reeks.

[harriechristus]

Oorspronkelijk geplaatst door Rizzz

Klopt, maar dit:

en dit:


is niet hetzelfde.

In beide gevallen gaat het om limietberekeningen maar in het 2de geval hebben we het over limieten naar oneindig, is dat niet waar we het over hadden?

En in het 2de geval (1/x) is 0 de limiet, niet oneindig.
We zeggen hier, "de limiet van 1/x als x oneindig benadert is 0"
Let op het woordje "benadert", maar niet "bereikt"

zie nogmaals:

http://www.mathsisfun.com/calculus/limits.html

Of de limiet nu oneindig is of 0 of welk willekeurig getal ook, dat doet er helemaal niet toe, het gaat om de oneindigheid, die uitwendig kan zijn bij het tellen van de natuurlijke getallen......dus: 1,2,3 enzovoort.
Of ook inwendig bij: 1, 1/2, 1/4, enzovoort tot 0

En die limiet wordt wel bereikt, zowel in ons verstand (want we weten wat de limiet is) als ook in werkelijkheid, want alle getallen zijn limieten.

En ook bij het eerste voorbeeld van een rechte lijn die van 1 naar 2 loopt is sprake van een limiet, namelijk steeds kleinere deeltjes tussen 1 en 2 in.
Namelijk 1, 1,5 1.9 1.99999999999999999........ enzovoort met als limiet 2, die inderdaad bereikt wordt.

[harriechristus]

Oorspronkelijk geplaatst door Rizzz

We hebben je op vele manieren aangetoond dat als je bewerkingen met oneindig toelaat, of delingen door 0 toelaat in de wiskunde, je allerlei tegenstrijdigheden tegen komt.

Dat is niet zo, want die zogenaamde tegenstrijdigheden zijn heel gemakkelijk op te lossen als je even je verstand gebruikt.
Bovendien zijn tegenstrijdigheden er om erkend te worden en opgelost.
Want de tegenstrijdigheid is de basis van de werkelijkheid.
Dat is namelijk dialectiek.

Vandaar dat we zeggen dat oneindig geen getal is en je niet mag delen door 0. Simpel toch?

Te simpel. De werkelijkheid is niet simpel.
eerst hadden de wiskundigen moeite met het accepteren van 0, toen met het accepteren van het oneindige als concept en nu weer met het accepteren van het oneindige als getal.

Je kan blijven rond de pot draaien

Je bedoelt dat je er zelf totaal niks van begrijpt en niet verder bent gekomen dan de rekenkunde van de kleuterschool.

maar het simpele feit blijft dat er geen "na" is in een oneindige reeks, da's per definitie zo, anders is het geen oneindige reeks.

Dat is volkomen onzin, wat heel gemakkelijk bewezen kan worden met de inwendige oneindigheid van een limietreeks.
Na 2 als limiet komt weer een nieuwe oneindige reeks, dus bijvoorbeeld 2,1 enzovoort.

En ook de wisundige Georg Cantor werkt met transfiniete getallen.

http://nl.wikipedia.org/wiki/Transfiniet_getal

[harriechristus]

136 - De paradox van de inwendige oneindigheid.

Hier openbaart zich een paradox der inwendige oneindigheid, dat als de toeschouwer meegaat met het steeds kleiner worden der afstand (en dus ook van de tijd), en dus ook zelf steeds kleiner wordt, dat de 0 van het limietpunt nooit bereikt wordt.
Maar voor degene die achterblijft, dus even groot blijft en ook zijn gewone traagheid der tijd behoudt, voltrekt het zich wel.

Zeno: Hercules en de schildpad.

Reeds de Griekse filosoof Zeno heeft dit beseft en het beroemde voorbeeld wat hij daarvan heeft gegeven is het verhaal van Hercules, die nooit een schildpad in zal kunnen halen, die eerst een bepaalde voorsprong heeft.
Want, zegt Zeno, als Hercules het punt heeft bereikt waar de schildpad eerst was, dan is de schildpad al een stukje verder en als Hercules ook dat punt heeft bereikt dan is de schildpad weer een nog kleiner stukje verder, enzovoort, tot in het oneindige.
Dus, is zijn redenatie: beweging kan eigenlijk helemaal niet bestaan, want elke beweging moet door een inwendige oneindigheid van steeds kleinere stukjes heen.
En vooral omdat elk stukje daarvan ook weer een inwendige oneindige verdeling heeft.
Eigenlijk kan je zelfs helemaal niet van je eigen plaats afkomen, want niemand kan zeggen welk het eerste punt is wat op een bepaald punt volgt.
Want tussen elke twee punten zijn oneindig veel andere punten mogelijk.
Dus wat is de eerste afstand vanaf de plaats waar Hercules begint met lopen?
Is dat 1 centimeter, dan kan dat niet, want daarvoor is sprake van een halve centimeter.
Dus dat komt eerst en daarvoor 1 millimeter en daarvoor nog kleiner, tot in het oneindige.
Dus een continue beweging is dan onmogelijk: elke beweging moet een verspringen zijn over een bepaalde afstand, hoe klein dan ook.

Bewegen als verspringen.

Maar een verspringen is geen echte beweging, maar een schijnbeweging, dus zoals ook een film van het ene beeld naar het andere springt en de schijn geeft een echte beweging te zijn.
Nu is het best mogelijk dat de beweging dan zo in elkaar zit als een verspringen, maar dan nog is daarmede het intellectuele probleem der inwendige oneindigheid als zodanig niet opgelost.
En ook het verspringen levert weer nieuwe problemen, namelijk hoe iets abrupt zou kunnen verdwijnen en in een andere plaats en tijd zomaar weer zou kunnen verschijnen.
Hoe lang duurt het dan voor iets verdwijnt, wat dan ook weer een bewegen (veranderen) zou zijn.
Dat iets in 0 seconde zou kunnen verdwijnen is niet minder paradoxaal dan de beweging dat is, die immers als limiet ook de 0 seconde heeft, die onbereikbaar is bij het constant delen.
Temeer daar dan ook nog eens sprake is van een overslaan van tussenliggende fases van ruimte en tijd en gestaltes, waarvoor geen verklaring is.
Dus de discrete beweging van punt naar punt in tijd en ruimte (dus als verspringen) is niet minder paradoxaal dan de continue beweging.

In de vorm van getallen.

In getallen omgezet hebben we voor de discrete beweging als verspringen de gehele getallen, dus: 1, 2, 3, enzovoort.
Waarbij de oneindig vele tussengetallen als breuken overgeslagen worden, die immers inwendig oneindig in aantal zijn.
Wat immers voorkomt in de limietreeks, dus als: 1/2, 1/4, 1/8, ... enzovoort, tot in het oneindige.
Oneindig gedeeld krijg je dan een continuüm, wat je ruimtelijk als een lijn voor kan stellen, terwijl de gehele getallen discreet zijn, apart als punten op die lijn.

De verzamelingsleer van Georg Cantor.

In de verzamelingsleer van Georg Cantor zijn die gehele getallen benoemd als de natuurlijke getallen (zonder negatieve getallen), maar samen met de negatieve getallen heten ze dan gehele getallen, en met de eindigende breuken erbij zijn het rationele getallen en met de oneindige breuken erbij zijn het reële getallen.
Als voorbeeld van oneindige breuken wordt dan pi = 3,141592653... enz. en wortel 2 = 1,414 213 562 ... enz genoemd.

[Rizzz]

Oorspronkelijk geplaatst door harriechristus

Of de limiet nu oneindig is of 0 of welk willekeurig getal ook, dat doet er helemaal niet toe, het gaat om de oneindigheid, die uitwendig kan zijn bij het tellen van de natuurlijke getallen......dus: 1,2,3 enzovoort.

De limiet is nooit oneindig, oneindig betekent dat er geen einde is, dus geen limiet, het woord zegt het zelf.

De rekenmachines zijn allemaal verkeerd, maar nu hebben we de woorden ook al verkeerd gekozen zeker?

[Rizzz]

Oorspronkelijk geplaatst door harriechristus

Dat is volkomen onzin, wat heel gemakkelijk bewezen kan worden met de inwendige oneindigheid van een limietreeks.

Doe dat dan eens want tot nu toe heb je ons enkel rare voorstellen gegeven waar we onmiddelijk gaten in geprikt hebben.